選択した画像 (a+b)^1/3 expansion 218490-(a+b)^1/3 expansion

About the Author Davneet Singh Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 9 yearsIf we make x and y equal to 1 in the following (Binomial Expansion) 11 We find the sum of the coefficients 12 Another way to look at 11 is that we can select an item in 2 ways (an x or a y), and as there are n factors, we have, in all, 2 n possibilities Sum of Coefficients for p Items Where there are p items 13• If the minterm expansion for f (A,B,C) = m 3 m 4 m 5 m 6 m 7, what is the maxterm expansion for f(A,B,C)?

How To Expand 1 X 3 In Series Quora

(a+b)^1/3 expansion

(a+b)^1/3 expansion-If we make x and y equal to 1 in the following (Binomial Expansion) 11 We find the sum of the coefficients 12 Another way to look at 11 is that we can select an item in 2 ways (an x or a y), and as there are n factors, we have, in all, 2 n possibilities Sum of Coefficients for p Items Where there are p items 13About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators

Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5

You will have 9(abc)>(abc) Now divide both sides by (abc), this leaves you with 9>1 which is correct 9 isIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial According to the theorem, it is possible to expand the polynomial n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive integer depending on n and b For example, 4 = x 4 4 x 3 y 6 x 2 y 2 4 x y 3 y 4 {\displaystyle ^{4}=x^{4}4x^{3}y6x^{2}y^{2}4xy^{3}y^{4}} TheHow do you use the binomial series to expand #f(x)=(1x)^(1/3 )#?

The power that we are expanding the bracket to is 3, so we look at the third line of Pascal's triangle, which is 1 3 3 1 So the answer is 3 3 3 × (3 2 × x) 3 × (x 2 × 3) x 3 (we are replacing a by 3 and b by x in the expansion of (a b) 3 above) GenerallyNoticias económicas de última hora, información de mercados, opinión y mucho más, en el portal del diario líder de información de mercados, economía y política en españolThat is, for each term in the expansion, the exponents of the x i must add up to n Also, as with the binomial theorem, quantities of the form x 0 that appear are taken to equal 1 (even when x equals zero) In the case m = 2, this statement reduces to that of the binomial theorem Example The third power of the trinomial a b c is given by

A Properties of the Binomial Expansion (a b) n There are `n 1` terms The first term is a n and the final term is b n Progressing from the first term to the last, the exponent of a decreases by `1` from term to term while the exponent of b increases by `1` In addition, the sum of the exponents of a and b in each term is nQuestion 10 Find the ratio of the 5 th term from the beginning to the 5 th term from the end in the binomial expansion of 2 1/3 1/{2(3) 1/3} 10 Solution Question 11 Find the coefficient of a 3 b 2 c 4 d in the expansion of (abcd) 10 SolutionDecimal Expansion The decimal expansion of a number is its representation in base10 (ie, in the decimal system) In this system, each "decimal place" consists of a digit 09 arranged such that each digit is multiplied by a power of 10, decreasing from left to right, and with a decimal place indicating the s place For example, the number with decimal expansion is defined as

2

Cube Root By Binomialexp

If we make x and y equal to 1 in the following (Binomial Expansion) 11 We find the sum of the coefficients 12 Another way to look at 11 is that we can select an item in 2 ways (an x or a y), and as there are n factors, we have, in all, 2 n possibilities Sum of Coefficients for p Items Where there are p items 13That is, for each term in the expansion, the exponents of the x i must add up to n Also, as with the binomial theorem, quantities of the form x 0 that appear are taken to equal 1 (even when x equals zero) In the case m = 2, this statement reduces to that of the binomial theorem Example The third power of the trinomial a b c is given byWe can get the identity for tan(A − B) by replacing B in (16) by −B and noting that tangent is an odd function tan(A−B) = tanA−tanB 1tanAtanB (17) 8 Summary There are many other identities that can be generated this way In fact, the derivations

In The Expansion Of X 2 1 3x 9 The Term Without X Is Equal

Plos One Soil Quality Indexing Strategies For Evaluating Sugarcane Expansion In Brazil

A1/3 a1/3 a1/3 = a (24) (a1/3)3 = a (25) (a2)1/3 = (a1/3)2 = a2∕3 (26) (a1/3)1/4 = a1/3 1/4 = (a1/4)1/3 (27) (a b)1/3 = a1/3 b1/3 (28) (a / b)1/3 = a1/3 / b1/3 (29) (1 / a)1/3 = 1 / a1/3 = a1/3 (30) Sponsored Links Mathematics Mathematical rules and laws numbers, areas, volumes, exponents, trigonometric functions and moreHow do you find the coefficient of x^5 in the expansion of (2x3)(x1)^8?If we want to expand (ab)3 we select the coefficients from the row of the triangle beginning 1,3 these are 1,3,3,1 We can immediately write down the expansion by remembering that for each new term we decrease the power of a, this time starting with 3, and increase the power of b So (ab) 3= 1a 3a2b3ab2 1b3 which we would normally write

Adv Bionomial Theorem Paper 01 1 Abstract Algebra Combinatorics

1 Evaluate The Following Determinants By The Process Of E Scholr

Exponents of (ab) Now on to the binomial We will use the simple binomial ab, but it could be any binomial Let us start with an exponent of 0 and build upwards Exponent of 0 When an exponent is 0, we get 1 (ab) 0 = 1 Exponent of 1The change expands the child tax credit, increasing the payouts to $3,600 for each child under six, and $3,000 for children six to 17 The payments, which are only available to families meetingEg, F(A,B,C) = ΠM(0,2,4) = Σm(1,3,5,6,7) Minterm expansion of F to minterm expansion of F' use minterms whose indices do not appear

Alg2 March28 The Answers

Www Acpsd Net Cms Lib Sc Centricity Domain 21 8 4 Pdf

And divide it by 1 more than the exponent of b That is the coefficient of a n − 4 b 4 Example 5 Use the binomial theorem to expand (a b) 8 SolutionThe expansion will begin (a b) 8 = a 8 8a 7 bThe first coefficient is always 1= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 15 6 1 1 7 21 35 35 21 7 1 Combinations Combinations will be discussed more fully in section 76, but here is a brief summary to get you going with the Binomial Expansion Theorem

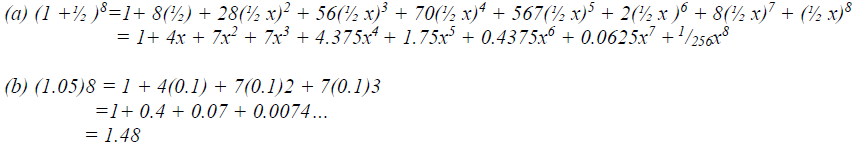
A Expand And Simplify The Binominal Expression 1 X Sup 8 Sup B Use The Expansion Up To The Fourth Term To Evaluate 1 05 Sup 8 Sup To 2

Resources Finalsite Net Images V Carrollwood Efz6tlshsjqxvh5hssrb Mathhlprep Pdf

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us CreatorsThe Binomial Theorem How to expand brackets with fractional powers easily using the general binomial expansionEssential maths revision video for Alevel aFind an answer to your question What are the coefficients for the binomial expansion of (a b)3?

2

The Binomial Expansion

Free math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantlyHow do you find the coefficient of x^6 in the expansion of #(2x3)^10#?If we want to expand (ab)3 we select the coefficients from the row of the triangle beginning 1,3 these are 1,3,3,1 We can immediately write down the expansion by remembering that for each new term we decrease the power of a, this time starting with 3, and increase the power of b So (ab) 3= 1a 3a2b3ab2 1b3 which we would normally write

2

What Is The Expansion Of A B C 3 Quora

A 3 b 3 We already know the formula/expansion for (a b) 3 Sum of all three digit numbers formed using 1, 3, 4 Sum of all three four digit numbers formed with non zero digits Sum of all three four digit numbers formed using 0, 1, 2, 3In this section we will give the Binomial Theorem and illustrate how it can be used to quickly expand terms in the form (ab)^n when n is an integer In addition, when n is not an integer an extension to the Binomial Theorem can be used to give a power series representation of the term(a 1/3 – b 1/3) ( a 2/3 a 1/3 b 1/3 b 2/3) Thank you!

Connect Issaquah Wednet Edu Staff Ihs Karpenkol Algebra Ii M Documents Download

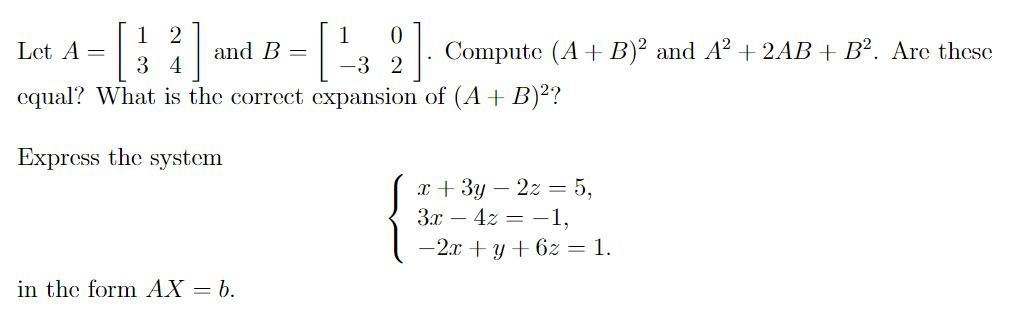
Solved 1 211 01 Let A Compute A B 2 And 2 Ab Chegg Com

Choose those not present in the minterms –So the Maxterm expansion for f(A,B,C) = M 0 M 1 M 2 Chap 4 CH10 Complement of minterm • Complement of a minterm is theAbstract Minimal cluster expansion models of Bsite cation ordering in A(B' 1/3,B'' 2/3)O 3 perovskites are evaluated It is demonstrated that the linear triplet interaction is both necessary and sufficient to stabilize the P3̄m1 12 structure ground state that is observed in such compounds as Ba(Zn 1/3,Nb 2/3)O 3 and Ba(Zn 1/3,Ta 2/3)O 3The linear triplet model exhibits a P3̄m1>Pm3̄m4 Binomial Expansions 41 Pascal's riTangle The expansion of (ax)2 is (ax)2 = a2 2axx2 Hence, (ax)3 = (ax)(ax)2 = (ax)(a2 2axx2) = a3 (12)a 2x(21)ax x 3= a3 3a2x3ax2 x urther,F (ax)4 = (ax)(ax)4 = (ax)(a3 3a2x3ax2 x3) = a4 (13)a3x(33)a2x2 (31)ax3 x4 = a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x)n come from the nth row of Pascal's

Ex 8 2 10 Coefficients Of R 1 R R 1 In 1 3 5

Http Imathesis Com Media Cambr Practice12 Pdf

∛a = a 1/3 n √a = a 1/n a p a q = a p q a p / a q = a p q a p b p = (ab) p (a p ) q = a pq Decimal Expansion;Pascal's triangle can be used to find the coefficient of binomial expansion (a b) 0 1 (a b) 1 1 1 (a b) 2 1 2 1 (a b) 3 1 3 3 1 (a b) 4 1 4 6 4 1 (a b) 5 1 5 10 10 5 1 (a b) 6 1 6 15 15 6 1LED began discussions with Shintech about the potential expansions in To secure the project, the State of Louisiana offered a competitive incentive package that includes the comprehensive solutions of LED FastStart ® – the nation's No 1 state workforce development program for the past 11 years The state has offered Shintech a performancebased grant of up to $66 million for the

Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5

2

The calculator will find the binomial expansion of the given expression, with steps shown Show Instructions In general, you can skip the multiplication sign, so `5x` is equivalent to `5*x`Write 13 as a binomial (1 __) Complete the expansion of (a b)6 with a = 1 and b = 03 (1 03)6 = (1)6 6(1)5(03) 15(1)4(03)2(1)3(03)315(1)2(03)4 6(1)(03)5 (03)6 After evaluating the powers, the expression reduces to =B, Property Condition and Quality of Construction of the Improvements (04/15/14) finish and/or structural changes have been made that increase utility and appeal through complete replacement and/or expansion A remodeled area reflects fundamental changes that include multiple alterations These alterations may include some or all

A B 1 3 Expansion

The Binomial Theorem

Expansions Which Have LogarithmBased Equivalents Summantion Expansion Equivalent Value Comments x nTo find an expansion for (a b) 8, we complete two more rows of Pascal's triangle Thus the expansion of is (a b) 8 = a 8 8a 7 b 28a 6 b 2 56a 5 b 3 70a 4 b 4 56a 3 b 5 28a 2 b 6 8ab 7 b 8 We can generalize our results as follows The Binomial Theorem Using Pascal's Triangle1 Determinants by M Bourne Before we see how to use a matrix to solve a set of simultaneous equations, we learn about determinants A determinant is a square array of numbers (written within a pair of vertical lines) which represents a certain sum of products Below is an example of a 3 × 3 determinant (it has 3 rows and 3 columns)

Madasmaths Com Archive Maths Booklets Standard Topics Various Binomial Series Expansions Exam Questions Pdf

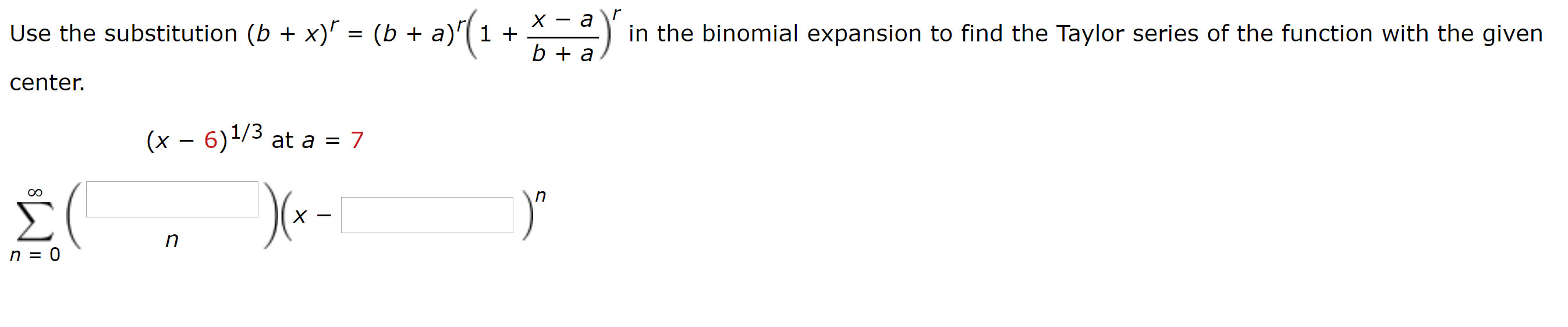
Solved Use The Substitution B X B 1 X Ar In Chegg Com

Find an answer to your question What are the coefficients for the binomial expansion of (a b)3?Binomial theorem works for non negative integer n ( a b) 1 3 = a 1 3 ( 1 b / a) 1 3 = a 1 3 ( 1 b 3 a − b 2 9 a 2 ) As User GIMUSI already told you, use his method to get a writing of that kind in order to use then In your case α = 1 / 3Hello there, I've always thought that the hardest part of any math problem is understanding the problem itself You've given us an expression, but there are lots of things that we could do with it First go back and make sure you understand what the problem is asking you to do

The Binomial Theorem Fractional Powers Expanding 1 2x 1 3 Youtube

Binomial Forms Expansion Of Binomial Expressions Ppt Download

Flexicraft Industries manufactures all types of metal expansion joints, rubber expansion joints, and other expansion joints for piping, as well as other related Flexible Piping Solutions and other piping related products Request HelpRailroad tracks and bridges, for example, have expansion joints to allow them to freely expand and contract with temperature changes, as shown in Figure \(\PageIndex{1}\) Figure \(\PageIndex{1}\) (a) Thermal expansion joints like these in the (b) Auckland Harbour Bridge in New Zealand allow bridges to change length without bucklingO 1, 4, 6, 4, 1 O 1,1 O 1, 2,1 O 1,3,3, 1

How To Expand 1 X 3 In Series Quora

First Level 01 Rational Number Number Theory

See all questions in The Binomial Theorem Impact of this question views around the worldIf a,b, and c are all real positive numbers then it will be correct But anyway to prove this without knowing anything factor out the 3 in the portion on the right You will have 27(abc)>3(abc), then divide both sides by 3;O 1, 4, 6, 4, 1 O 1,1 O 1, 2,1 O 1,3,3, 1

2

Msbshse Solutions For Class 8 Maths Part 1 Chapter 5 Expansion Formulae Download For Free

Shintech's plant complex near Plaquemine has been the site for a $14 billion expansion The company is now planning another $13 billion investment at its Plaquemine and Addis facilities1 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials informationIn this section we will give the Binomial Theorem and illustrate how it can be used to quickly expand terms in the form (ab)^n when n is an integer In addition, when n is not an integer an extension to the Binomial Theorem can be used to give a power series representation of the term

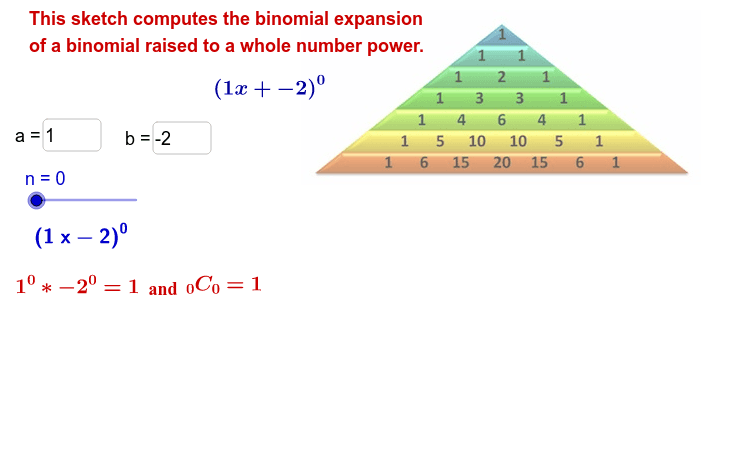
Binomial Expansion Geogebra

Write The Following Cubes In Expanded Form 2 X 1 Whole Cube Math Polynomials Meritnation Com

Why create a profile on Shaalaacom?

Sequences And Series Algebra And Trigonometry

Ppt The Coefficients In The Binomial Expansion Of 1 X 5 Powerpoint Presentation Id

The Last Term In The Binomial Expansion Of 2 1 3 1 Sqrt 2 N Is 1 3 9 1 3 Log 3 Youtube

4 The Binomial Theorem

What Is A B 3 Quora

2

U6 Binomial Expansion 1 F X X

Binomial Theorem Task Let S Experiment And See If You See Anything Familiar Expand These Binomials If Your Last Name Begins With A F A B 0 If Your Ppt Download

Www Lcps Org Cms Lib Va Centricity Domain Unit 11 day 2 precalc 1718 jw completed Pdf

Write The Following Cubes In Expanded Form I 2x 1 3 Ii 2a 3b 3 Sarthaks Econnect Largest Online Education Community

Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5

Maths M1 Chp1 Binomial Ans By Patrick Ho Issuu

Page 1 1 The Decimal Expansion Of Number 2 441 2 5 7 Has A

Http Fchsmrshaley Weebly Com Uploads 1 7 6 5 Section 3 2 Pascals Triangle And Binomial Expansion Pdf

2

Http Cavanagh Pbworks Com W File Fetch 6275 5 2 binomial theorem nov 26 Pdf

A B 1 3 Expansion

2

Pascal S Tri Binomial Expansion Geogebra

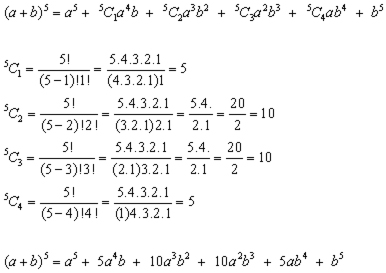
The Binomial Theorem Algebra Pure Mathematics From A Level Maths Tutor

Http Www2 Mae Ufl Edu Uhk Binomial Expansion Pdf

Q Tbn And9gcrswdldblxmiitn Ggstx6knbcgxw3sex0r673zeswoh Igfkvn Usqp Cau

Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A

2

Http Pnhs Psd2 Org Documents Tacosta Pdf

2 3 X Pla Can Be Expanded In Ascending Powers Of X If Math

6 Binomial Theorem

A B 1 3 Expansion

A Lesson In Making Use Of Structure From With Jmccalla1 Experiments In Learning By Doing

Pure Maths Ch8 Flashcards Quizlet

2

Search Q Binomial Expansion For Negative Fractional Powers Tbm Isch

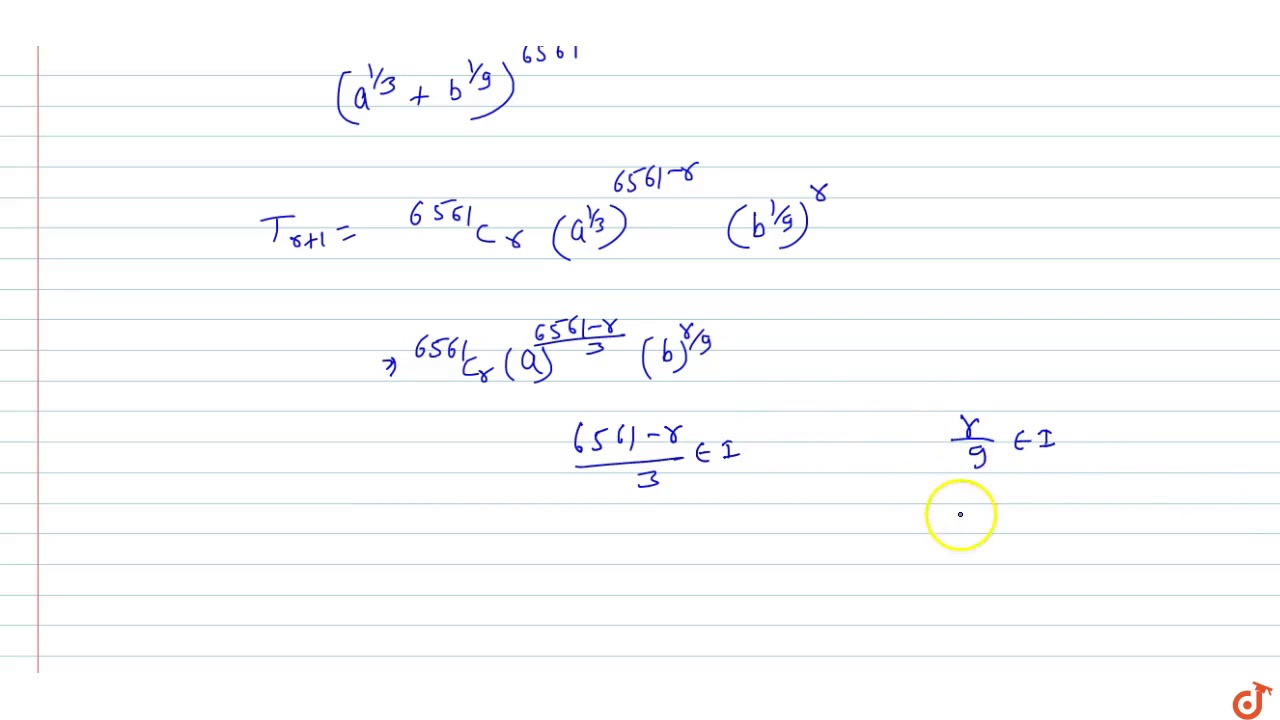
In The Expansion Of A 1 3 B 1 9 6561 Where A And B Are Distinct Prime Numbers Youtube

In The Expansion Of A B Anul Uie Expansiitutu A 3 B 4c 5in

Illustration Of A Two Dimensional 1 3 Gradual Planar Expansion Download Scientific Diagram

Solved Engineering Analysis Of The Gas Expansion Factor Chegg Com

Determinants And Linear Transformations 4 A Let A Be The Matrix 1 2 4 1 3 2 11 I Calculate The Determinant Of A Us Homeworklib

Q Tbn And9gcrshlwp5l1m2u84p6hz6fecz0jxrhldtrtkz9e Offkzxulvyrd Usqp Cau

2

X Y 2 B 1 1 Dxth 1 Dyth Th B 2 2 Dxth 2 Dyth Optimal Asymptotic Download Scientific Diagram

Binomial Theorem Derived Copy Of Precalculus Openstax Cnx

Elie Maths Ib Maths Sl Blog Binomial Expansion

A B 1 3 Expansion

Solution Use The Binomial Theorem To Expand The Binomial And Express The Result In Simplified Form X 4 3

Www Anderson5 Net Cms Lib Sc Centricity Domain 2175 Hw 1a binomial expansion using pascals triangle key Pdf

Webpages Uncc Edu Sjbirdso Calc ii Spr15 Quizzes Finalfall14solution Pdf

The Coefficient Of An In The Expansion Of 21 1 3 Em 1 2 31 3 1 B 1 3n 2 2n 3 1 C I 2n 3 3n 2 1 None Of These

Lesson 7 Expanding Products Of Algebraic Expressions Binomial Expansion Brilliant Maths

Amazon Com Smead One Inch Expansion Fastener Folder 1 3 Top Tab Legal Gray Green 25 Box Smd By Sm Office Products

Shortcut To Binomial Expansion

Fastener Folder 1 Expansion 1 3 Top Tab Letter Gray Green 25 Box

1

Expand Spin Hamiltonian

If 4th Term In The Expansion Of Ax 1 X N Is 5 2 Then The Values Of A And N A 1 2 6 B 1 3 C Brainly In

6 Find The Coefficient Of X N In The Polynomial Left X N C 0 Right Left X

Madasmaths Com Archive Maths Booklets Standard Topics Various Binomial Series Expansions Exam Questions Pdf

2

Binomial Theorem And Binomial Series 10 3 Sideway Output To

Www Amphi Com Cms Lib Az Centricity Domain 256 3 2b multiplying polynomials Pdf

Find The 13th Term In The Expansion Of 9x 1 3 X 18 X 0 Sarthaks Econnect Largest Online Education Community

Mt50 Advanced Linear Algebra Project Laplace S Expansion And

Wolfram Alpha Examples Step By Step Solutions

Using Binomial Theorem Write Down The Expansions Of The Following 1 3x 7

Expanding Brackets Using Pascal S Triangle Youtube

Can You Expand This Using Partial Fractions Found By Using X 1 3 Or Is It Not Valid As X 1 3 Maths

Web Pa Msu Edu People Pratts Phy231 Exams Extraproblems Ch10 Pdf

Ext Math Bio 241 Biology Studocu

Hhsmathslyr2 Files Wordpress Com 16 09 2 7 Binomial Expansions Lesson Pdf

Pascal Triangle For Cat Exam Preparation Math Methods Math Tutorials Studying Math

Out Of 1 In 1 Attempts Write The Following Number In Expanded Form 6814 Course Hero

Binomial Theorem Wikipedia

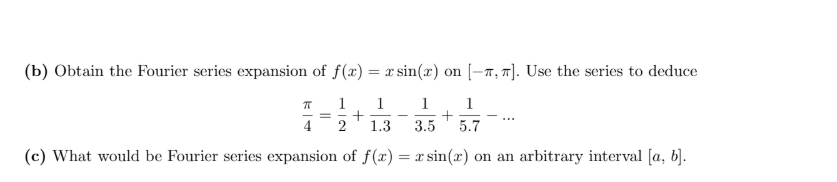
Answered B Obtain The Fourier Series Expansion Bartleby

Incoming Term: (a+b)^1/3 expansion,